Unveiling The Power Of Logic: Truth Tables And Karnaugh Maps In Digital Design
Unveiling the Power of Logic: Truth Tables and Karnaugh Maps in Digital Design
Related Articles: Unveiling the Power of Logic: Truth Tables and Karnaugh Maps in Digital Design
Introduction
With enthusiasm, let’s navigate through the intriguing topic related to Unveiling the Power of Logic: Truth Tables and Karnaugh Maps in Digital Design. Let’s weave interesting information and offer fresh perspectives to the readers.
Table of Content
Unveiling the Power of Logic: Truth Tables and Karnaugh Maps in Digital Design

In the realm of digital design, where information flows in the form of binary digits (bits), the ability to represent and manipulate logic functions is paramount. Truth tables and Karnaugh maps (K-maps) emerge as essential tools, providing a clear and concise framework for understanding, simplifying, and implementing logical expressions. This article delves into the intricacies of these tools, highlighting their individual strengths and the synergistic relationship they forge in the pursuit of efficient digital circuit design.
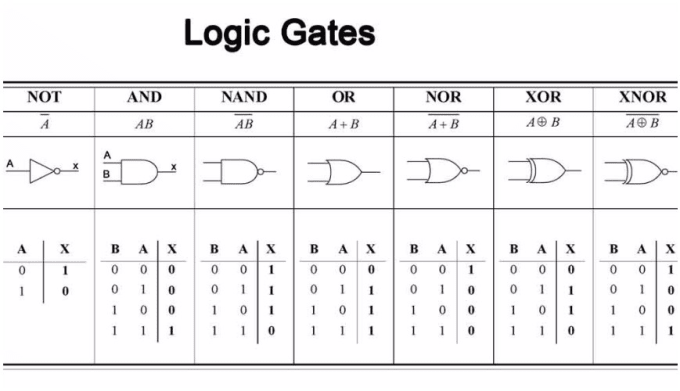
Truth Tables: The Foundation of Logic
A truth table is a tabular representation of a Boolean function, meticulously outlining the output value for every possible combination of input values. It serves as a fundamental building block in digital design, providing a comprehensive and unambiguous definition of the function’s behavior.
Constructing a Truth Table
Consider a Boolean function with ‘n’ input variables. Each variable can assume either a ‘0’ or ‘1’ value, resulting in 2^n possible input combinations. The truth table comprises a column for each input variable and an additional column for the output. Each row represents a unique input combination, and the corresponding output value is listed in the output column.
Example:
Let’s analyze the function F(A, B, C) = AB + AC.
| A | B | C | F(A, B, C) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
The truth table reveals that the output ‘F’ is ‘1’ when A is ‘1’ and either B or C is ‘1’, and ‘0’ otherwise.
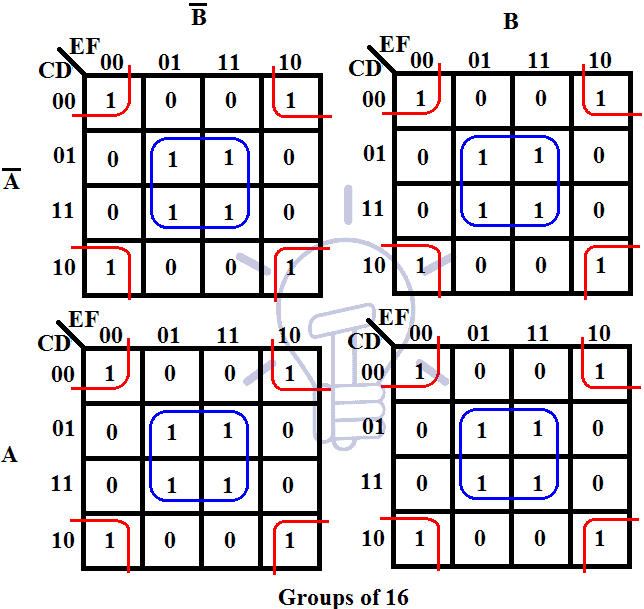
Karnaugh Maps: Visualizing Logic Simplification
While truth tables provide a thorough representation of logical functions, their usefulness in simplifying complex expressions is limited. Enter the Karnaugh map (K-map), a visually intuitive tool that facilitates the simplification of Boolean expressions by exploiting the concept of adjacent minterms.
The Structure of a K-map
A K-map is a grid-like representation of a Boolean function, where each cell corresponds to a unique minterm (a product term consisting of all input variables in their literal or complemented form). The arrangement of cells is crucial, ensuring that adjacent cells differ in only one variable. This arrangement allows for the identification of groups of adjacent minterms, leading to simplification.
Example:
Let’s consider the same function F(A, B, C) = AB + AC.
AB
C 00 01 11 10
-------------------
0 | 0 0 1 1
-------------------
1 | 0 1 1 1
-------------------The K-map represents the function with ‘1’ in the cells corresponding to the minterms AB and AC.
Simplifying with K-maps
The simplification process involves identifying groups of adjacent ‘1’s in the K-map. These groups can be rectangular or square, with powers of 2 cells (1, 2, 4, 8, etc.). Each group represents a simplified product term, where the variables that remain constant within the group are included in the term, and the variables that change are excluded.
In our example, the two ‘1’s form a group of two adjacent cells, leading to the simplified expression F(A, B, C) = A.
The Power of K-maps
K-maps provide a powerful visual aid for Boolean expression simplification, offering several advantages over truth tables:
- Visual Representation: The grid format allows for a clear and intuitive visualization of the function’s behavior, making it easier to identify patterns and simplify expressions.
- Adjacent Minterm Identification: The arrangement of cells ensures that adjacent cells differ in only one variable, facilitating the identification of groups of adjacent minterms, leading to simplification.
- Minimized Expression: K-maps enable the derivation of minimal expressions, reducing the number of literals and gates required in the implementation of the function, resulting in more efficient and cost-effective circuits.
Truth Tables and K-maps: A Symbiotic Partnership
While truth tables and K-maps offer distinct advantages, they complement each other effectively. Truth tables serve as the foundation, providing a comprehensive definition of the function. K-maps then leverage this information to visually simplify the expression, minimizing the logic required for implementation.
Truth Table to K-map Conversion
The process of converting a truth table to a K-map involves mapping each row of the truth table to the corresponding cell in the K-map. The cell receives a ‘1’ if the corresponding row in the truth table has a ‘1’ in the output column, and a ‘0’ otherwise.
K-map to Boolean Expression Conversion
Once the K-map is populated, the process of deriving the simplified Boolean expression involves identifying groups of adjacent ‘1’s and writing down the product term corresponding to each group. The final expression is obtained by ORing these product terms.
Applications in Digital Design
The combined power of truth tables and K-maps is crucial in various aspects of digital design:
- Logic Circuit Design: They enable the efficient design of logic circuits, minimizing the number of gates required for implementing a specific function, leading to more cost-effective and compact circuits.
- Boolean Function Simplification: They provide a systematic method for simplifying complex Boolean expressions, reducing the complexity of the circuit and enhancing its performance.
- Digital System Verification: They facilitate the verification of digital circuits by ensuring that the implemented logic matches the desired functionality.
FAQs about Truth Tables and K-maps
Q1: What is the maximum number of input variables that can be handled by a K-map?
A: The maximum number of input variables that can be effectively handled by a K-map is 4. For higher numbers of variables, the visual representation becomes increasingly complex, making simplification less intuitive.
Q2: Can K-maps be used to simplify functions with don’t care conditions?
A: Yes, K-maps can be used to simplify functions with don’t care conditions. Don’t care conditions represent input combinations for which the output value is irrelevant. These conditions can be used to further simplify the expression by including them in groups of adjacent ‘1’s.
Q3: How do truth tables and K-maps contribute to the optimization of digital circuits?
A: Truth tables and K-maps contribute to the optimization of digital circuits by enabling the simplification of Boolean expressions, reducing the number of gates required for implementation. This leads to smaller, faster, and more cost-effective circuits.
Tips for Effective Use of Truth Tables and K-maps
- Start with a Truth Table: Always begin by constructing a truth table to fully understand the function’s behavior.
- Choose the Appropriate K-map: Select the K-map size that corresponds to the number of input variables in the function.
- Identify Adjacent Groups: Focus on identifying the largest possible groups of adjacent ‘1’s in the K-map.
- Don’t Forget Don’t Cares: Include don’t care conditions in groups of adjacent ‘1’s to maximize simplification.
- Verify the Result: After deriving the simplified expression, verify its correctness by comparing its truth table with the original function’s truth table.
Conclusion
Truth tables and Karnaugh maps are indispensable tools in the arsenal of digital designers, providing a robust foundation for understanding and manipulating logic functions. Their symbiotic relationship ensures efficient design, simplification, and verification of digital circuits. By leveraging the power of these tools, engineers can create optimized digital systems that meet the demands of modern technology. While the world of digital design evolves at a rapid pace, the fundamental principles of logic embodied by truth tables and K-maps remain constant, ensuring their enduring relevance in the future.





Closure
Thus, we hope this article has provided valuable insights into Unveiling the Power of Logic: Truth Tables and Karnaugh Maps in Digital Design. We hope you find this article informative and beneficial. See you in our next article!